I’m a big fan of Andrew’s Gelman blog (http://andrewgelman.com/). I think that my statistical intuition is way much better after reading it. For example, there’s a post about different types of errors in NHST, not limited to the widely known Type I and Type II errors - http://andrewgelman.com/2004/12/29/type_1_type_2_t/. You should read this before continuing because the rest of this post will be based on it, and the article which is linked in that post (http://www.stat.columbia.edu/~gelman/research/published/francis8.pdf).
The code below performs the simulation described at the beginning of the third paragraph of the “Type S error rates for classical and Bayesian single and multiple comparison procedures” article.
simulation <- function(tau, sigma, n = 2000) {
# simulate the data as described at the begining of the 3rd paragraph.
result <- t(replicate(n, {
dif <- rnorm(n = 1, sd = 2 * tau)
yy <- rnorm(1, dif, 2 * sigma)
c(dif, yy)
}))
bThreshold <-
1.96 * sqrt(2) * sigma * sqrt(1 + (sigma ^ 2) / (tau ^ 2)) # Equation (6)
clasThreshold <- 1.96 * sqrt(2) * sigma # Equation (5)
yy <- result[, 2]
probConfClaimBayes <- mean(yy > bThreshold | yy < -bThreshold)
probConfClaimClas <-
mean(yy > clasThreshold | yy < -clasThreshold)
bayesConfClaim <- result[yy > bThreshold | yy < -bThreshold,]
bayesConfClaim <- sign(bayesConfClaim)
sErrorCondClaimBayes <-
mean(bayesConfClaim[, 1] != bayesConfClaim[, 2])
clasConfClaim <-
result[yy > clasThreshold | yy < -clasThreshold,]
clasConfClaim <- sign(clasConfClaim)
sErrorCondClaimClass <-
mean(clasConfClaim[, 1] != clasConfClaim[, 2])
list(
data = result,
bThreshold = bThreshold,
clasThreshold = clasThreshold,
probConfClaimBayes = probConfClaimBayes,
probConfClaimClas = probConfClaimClas,
sErrorCondClaimBayes = sErrorCondClaimBayes,
sErrorCondClaimClass = sErrorCondClaimClass
)
}
format_result <- function(result) {
c(
sprintf("Prob of claim - Bayesian: %.2f%%", result$probConfClaimBayes * 100),
sprintf("Prob of claim - Classical: %.2f%%", result$probConfClaimClas * 100),
sprintf("Prob of S-error cond claim - Bayesian: %.2f%%", result$sErrorCondClaimBayes * 100),
sprintf("Prob of S-error cond claim - Classical: %.2f%%", result$sErrorCondClaimClass * 100))
}
plot_tresholds <- function(result, ...) {
plot(result$data, xlab = "theta_j - theta_k", ylab = "y_j - y_k", ...)
abline(h = c(-result$bThreshold, result$bThreshold), lty = 2, col = "green")
abline(h = c(-result$clasThreshold, result$clasThreshold), lty = 2, col = "red")
abline(v = 0, lty = 2)
legend("topleft", c("Bayesian Treshold", "Classical Treshold"), lwd = 2, lty = 1, col = c("green", "red"))
legend("bottomright", format_result(result))
}Here you can see the replicated plots from the page 7. I merged the Bayesian and Classical versions into one plot, and I also added the probabilities of claiming that there are differences and the conditional probability of S-Error given the claim.
Note that I got different values than those from figure 3, but the experimental setting might cause it (I’m not using equation described in the test to approximate the result), or I have an error in the code (but I cannot find one…). However, the main point of the article is still valid;)
set.seed(123)
plot_tresholds(simulation(0.5,1,2000), main = "tau: 0.5, sigma: 1")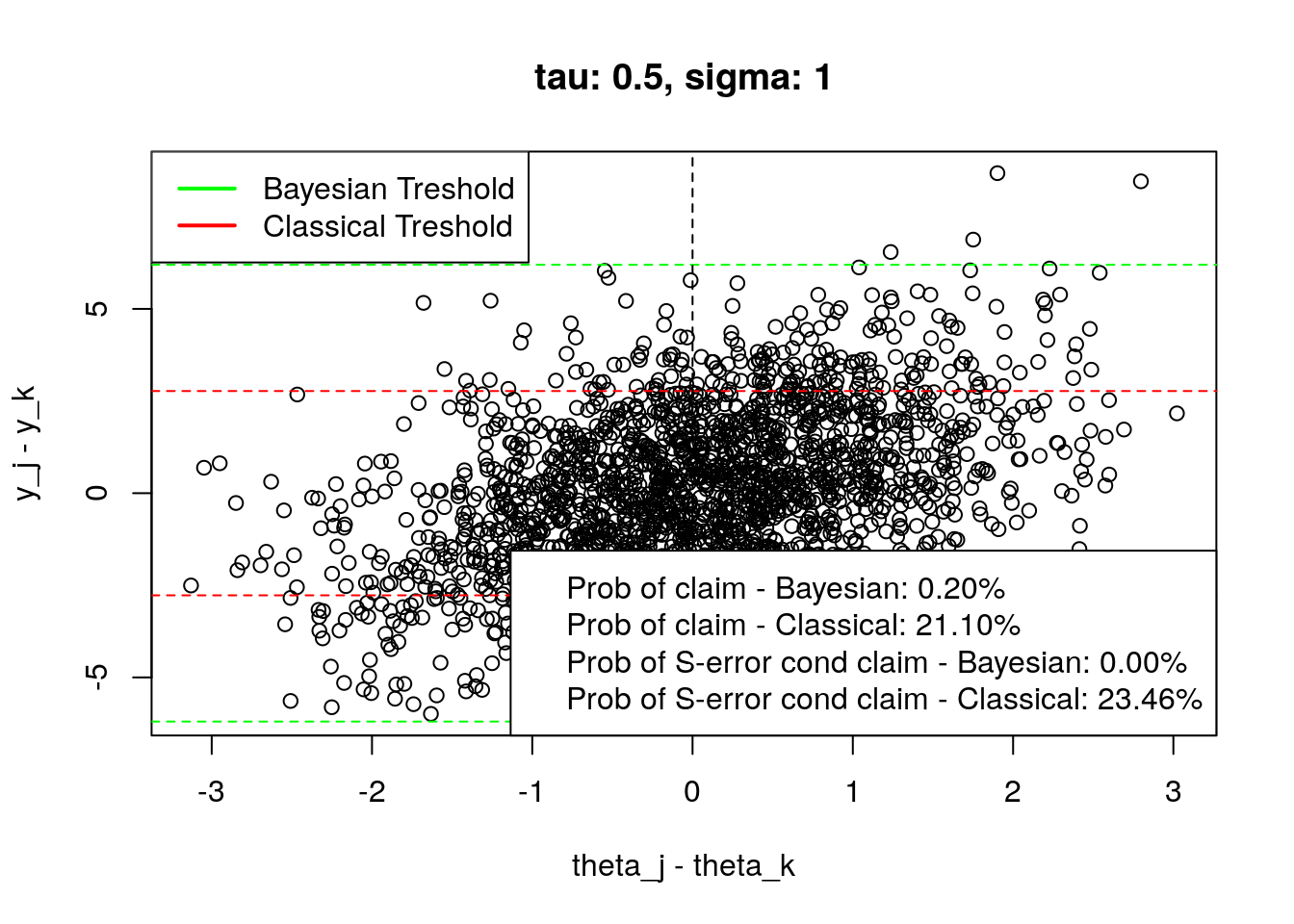
plot_tresholds(simulation(1,1,2000), main = "tau: 1, sigma: 1")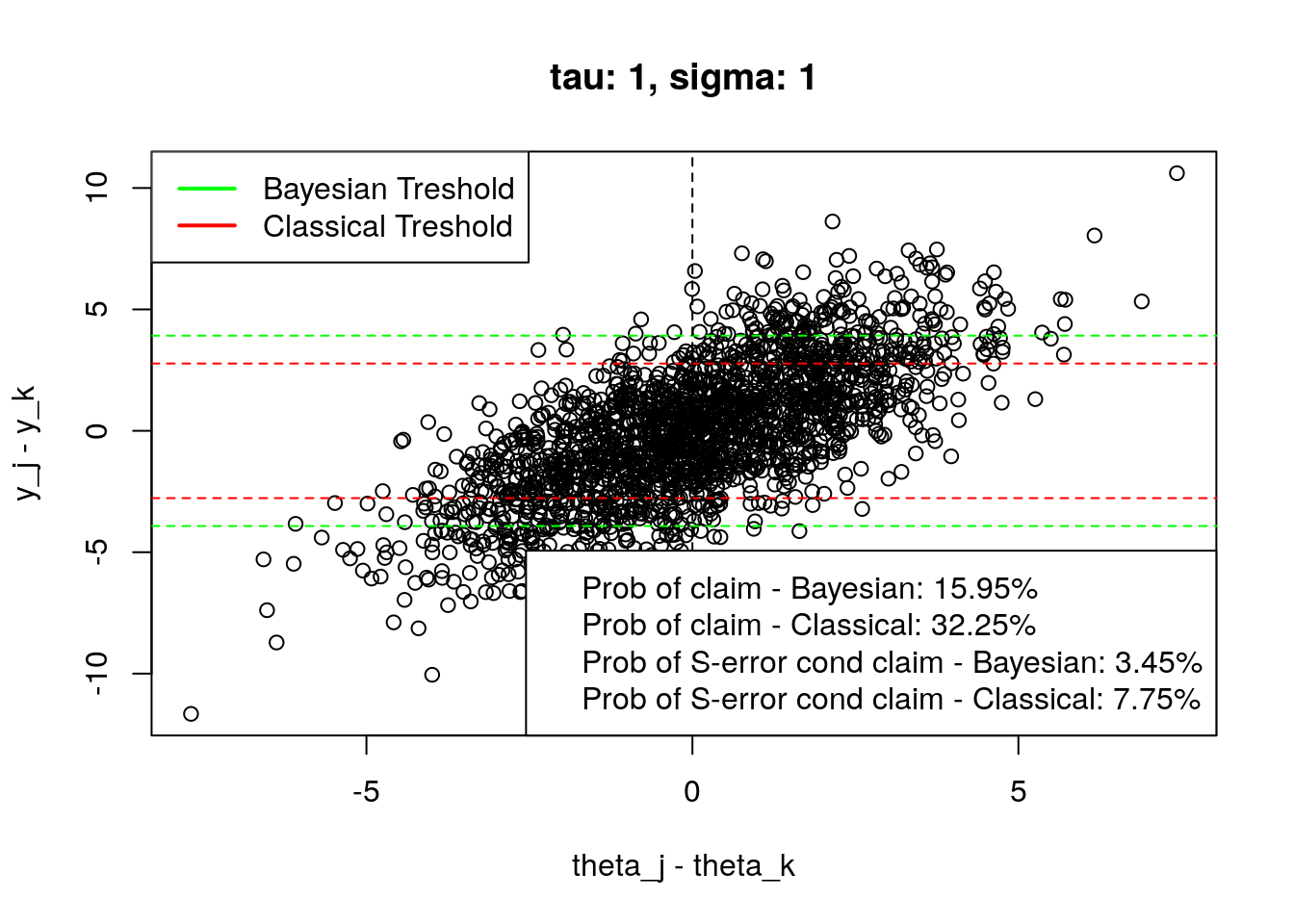
plot_tresholds(simulation(2,1,2000), main = "tau: 2, sigma: 1")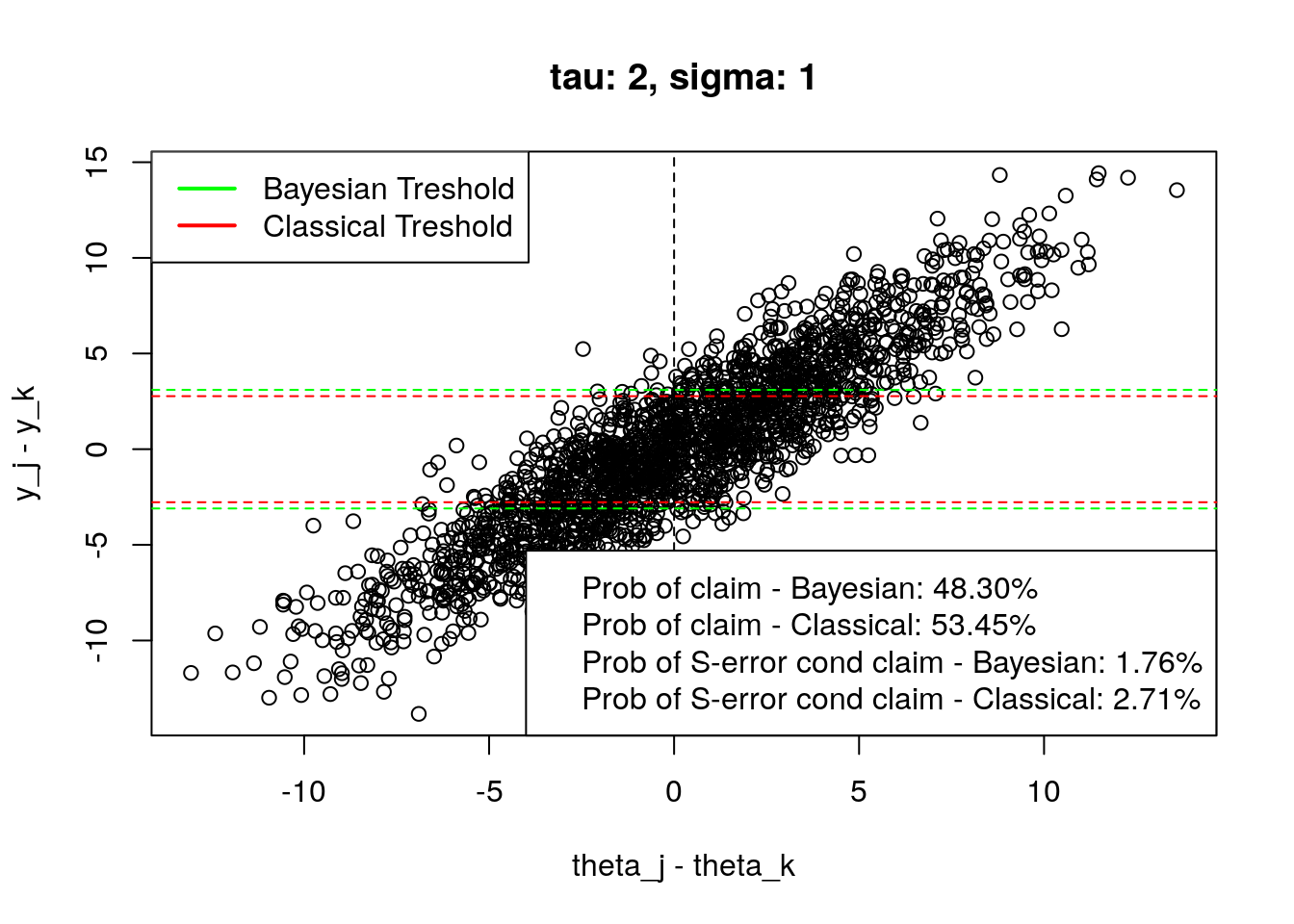
More resources on this topic:
If you want more information about S type errors or related topics check out the links below:
